Controles realizados los días 09-12-02 y 12-12-02
1.
Contesta
las siguientes preguntas:
a)
Define y formula momento de una fuerza.
b)
¿Qué
diferencia hay entre el coeficiente de rozamiento estático y el dinámico? ¿En
qué unidades del S.I. se expresa cada uno? ¿De qué depende la fuerza de
rozamiento entre dos superficies?
c)
Explica
el principio de conservación del momento lineal
2.
Un cuadro
tiene una masa de 5 kg y cuelga de dos cables que forman un ángulo de 400
con la horizontal (el techo). Si los cables son capaces de soportar una tensión
de 40N cada uno, ¿aguantarán el peso del cuadro?
3.
Tenemos
un ascensor de 800 kg en un edificio construido en la superficie de Marte.
Calcula:
a)
La intensidad del campo gravitatorio en la superficie de Marte.
b)
La tensión que soportaría el cable que sujeta el ascensor si este
asciende con una aceleración de 2 m·s-2.
Datos:
MMarte = 6,4·1023 kg ; RMarte = 3400 km
4.
Calcula
la velocidad a la que un camión puede tomar una curva de 400 m de radio si el
coeficiente de rozamiento entre los neumáticos y el suelo es de 0,8.
5.
Determinar
la aceleración del sistema y la tensión de la cuerda que une ambas masas.
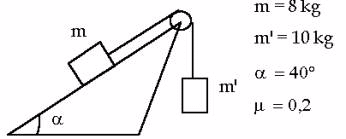
6.
Un objeto
explota y se rompe en dos trozos. Uno forma un ángulo de 60° con la horizontal
(20kg y v = 10 m/s). Calcula la velocidad del segundo (módulo, ángulo con la
horizontal). Se supone que el objeto inicial (antes de la explosión) tiene una
masa de 50 kg y se encuentra en reposo.
7.
Contesta
las siguientes preguntas:
a)
¿Qué relación hay
entre las dos primeras leyes de Newton?
b)
Escribe la fórmula e indica qué representa cada símbolo: ley de Hooke,
momento de una fuerza.
c)
Define
impulso mecánico y momento lineal. Escribe la relación entre ambos conceptos y
sus unidades en el S.I.
8.
Una lámpara
de 10 kg pende a 0,40 m del techo sujeta por dos cuerdas de 0,60 m cada una.
Dibuja el sistema con todas las fuerzas que actúan sobre la lámpara. Calcula
el ángulo que forman las cuerdas con la horizontal (el techo). Halla la tensión
que soporta cada cuerda.
9.
Calcula la tensión que soporta el cable de un ascensor de 800 kg que
asciende:
a)
Con una aceleración de 2 m·s-2.
b)
Frenando a razón de 3 m/s cada segundo.
10.
Un satélite da vueltas alrededor de Marte a una distancia de la
superficie del planeta de 100 km. Calcula la velocidad con que gira.
Datos:
MMarte = 6,4·1023 kg ; RMarte = 3400 km
11.
Determinar
la aceleración del sistema y la tensión de la cuerda.
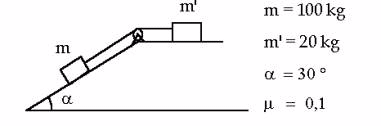
12.
Dos objetos
de masas m1 = 10 kg y m2 = 15 kg, chocan (v1
= 4 i - 2 j m/s
, v2 = 5 i +
7 j m/s). Suponiendo que
quedan unidos después del choque, calcula la velocidad del cuerpo que sale
despedido (módulo, ángulo respecto a la horizontal). Representa el sistema
antes y después del choque.