Preguntas realizadas en otros exámenes de Dinámica [1]
1.
Contesta las siguientes preguntas:
a)
¿Qué diferencia hay entre un sistema de referencia inercial y un
sistema de referencia no inercial?
b)
¿Qué es la intensidad gravitatoria? ¿En qué unidades se expresa?
c)
¿Qué diferencia hay entre masa inercial y masa gravitatoria?
d)
Define impulso mecánico y momento lineal. Escribe la relación entre
ambos conceptos y sus unidades en el S.I.
2.
La fuerza necesaria para abrir una puerta es la sexta parte de su peso,
aplicada perpendicularmente a dicha puerta en el tirador, situado en el centro
de la misma. Si la puerta es de 0,90 m de ancho y tiene una masa de 60 kg, ¿cuánto
valdrá la fuerza mínima necesaria para abrirla tirando perpendicularmente del
extremo en lugar del centro?
3. Calcula la aceleración del sistema (indica el sentido del movimiento) y la tensión de la cuerda:
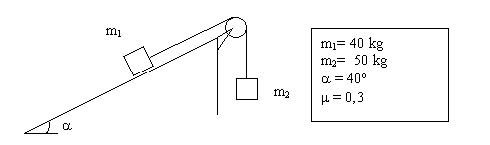
4.
Un ascensor sufre una aceleración de 1,5 m / s2, tanto al
subir como al bajar. Si el ascensor tiene una masa de 800 kg y la carga máxima
es de 400 kg ¿Qué tensión mínima deberá soportar el cable del ascensor sin
que se rompa?
5.
Se hace girar una honda de 60 cm en un plano vertical con una masa de 200
g en el extremo. Suponiendo que la velocidad de giro sea de 5 r.p.s., calcula la
tensión de la honda en el punto más alto y en el punto más bajo.
6.
Contesta las siguientes preguntas:
a)
¿Qué dice el principio de relatividad de Galileo?¿Qué son las fuerzas
de inercia?
b)
¿Qué diferencia hay entre el coeficiente de rozamiento estático y el
dinámico? ¿En qué unidades del S.I. se expresa cada uno? ¿De qué depende la
fuerza de rozamiento entre dos superficies?
c)
Define impulso mecánico y momento lineal. Escribe la relación entre
ambos conceptos y sus unidades en el S.I.
7.
Una barra de cinco metros está apoyada en su punto medio, sobre el que
puede girar libremente. Si se coloca una masa de 40 kg en uno de los extremos,
¿dónde se debe colocar otra masa de 60 kg para que el sistema no gire?
8. Calcula la aceleración del sistema (indica el sentido del movimiento) y la tensión de la cuerda. Véase el dibujo del problema 3 con estos datos: m1= 40 kg m2= 10 kg a = 40º m = 0,3
9.
Un ascensor sufre una aceleración de 1,5 m / s2, tanto al
subir como al bajar. Si el ascensor tiene una masa de 1200 kg y la carga máxima
es de 500 kg ¿Qué tensión mínima deberá soportar el cable del ascensor sin
que se rompa?
10.
Se hace girar una honda de 70 cm en un plano vertical con una masa de 500
g en el extremo. Suponiendo que la velocidad de giro sea de 6 r.p.s., calcula la
tensión de la honda en el punto más alto y en el punto más bajo.
11.
Contesta las siguientes preguntas:
d)
Nombra los cuatro tipos de interacciones básicas.
e)
¿Qué se tiene que cumplir para que un sistema se encuentre en
equilibrio?
f)
¿Qué relación hay entre la primera y la segunda leyes de Newton?
12.
Observa la figura siguiente:
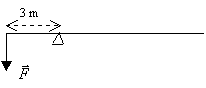
Si
F = 50 N, ¿dónde se debe situar otra fuerza para que el sistema no
gire? Dibuja la dirección y sentido. Calcula su situación y módulo.
13. Calcula la aceleración del sistema si la masa sobre la superficie horizontal tiene una masa de 20 kg
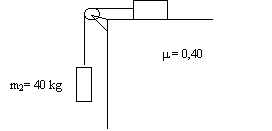
¿Hacia dónde se mueve?
14.
Un cable de acero resiste una carga máxima de 5000 N. ¿Cuál será la
aceleración máxima con que se puede elevar una masa de 400 kg colgada de este
cable antes de que se rompa?
15.
Contesta las siguientes cuestiones:
a)
¿Qué es la
intensidad gravitatoria? ¿En qué unidades se expresa?
b)
¿Qué diferencia
hay entre masa inercial y masa gravitatoria?
c)
Observa el gráfico.
¿En qué caso estará en equilibrio, con el c.d.g. en 1 ó en 2? ¿Por qué?
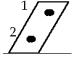
16.
Dos fuerzas paralelas de sentido contrario y módulos 7 y 15 N,
respectivamente, están aplicadas en los extremos de una barra de 1,5 m de
longitud. Calcular las características de la fuerza resultante.
17.
Determinar la aceleración del sistema y la tensión de la cuerda.
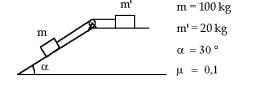
18.
Se hace girar una honda de 75 cm en un plano vertical con una masa de 200
g en el extremo. Suponiendo que la velocidad de giro sea de 15 m/s, calcular la
tensión de la honda en el punto más alto y en el punto más bajo.
19.
Un camión viaja con una velocidad
![]() m/s, y choca con un vehículo que lleva una velocidad
m/s, y choca con un vehículo que lleva una velocidad
![]() m/s. Si mcamión
= 7500 kg y mvehículo =
1500 kg, ¿cuál será la velocidad (módulo y ángulo respecto a la horizontal)
de los despojos de ambos si permanecen enganchados después del choque?
m/s. Si mcamión
= 7500 kg y mvehículo =
1500 kg, ¿cuál será la velocidad (módulo y ángulo respecto a la horizontal)
de los despojos de ambos si permanecen enganchados después del choque?
20.
Determinar la aceleración del sistema y la tensión de la cuerda que une
ambas masas.
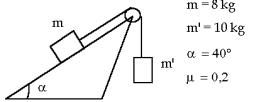
21.
Calcula el coeficiente de rozamiento neumáticos-suelo para que un vehículo
de 1,1 t tome una curva de radio de giro 100 m a 60 km/h sin salirse de la
carretera.
22.
Un objeto de 36 kg que se encuentra en reposo explota y se rompe en dos
trozos. Uno forma un ángulo de 130° respecto a la horizontal ( 8 kg y v
= - 5,14 i + 6,13 j m/s). Calcular la velocidad del segundo (módulo
y ángulo con respecto a la horizontal). Dibuja el sistema.
23.
Contesta las siguientes preguntas:
a)
¿Qué relación
existe entre el momento de una fuerza respecto a un punto y el equilibrio de los
cuerpos?
b)
Escribe la ecuación
que representa g.
c)
¿Qué es el
centro de gravedad?
d)
¿Qué son las
fuerzas inerciales? Pon dos ejemplos de fuerzas inerciales.
24.
Tenemos dos fuerzas paralelas del mismo sentido de valores 6 y 10 N,
respectivamente. ¿Qué fuerza debemos hacer para equilibrar el sistema? ¿Hacia
dónde se dirigirá? Si la fuerza que debemos hacer para equilibrar el sistema
se encuentra a 3 m de la mayor, ¿a qué distancia se encontrará de la pequeña?
25.
Calcula la tensión de la cuerda y la aceleración del sistema.
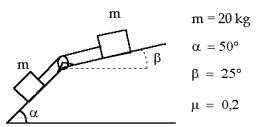
26.
Queremos subir un montacargas al completo (900 kg) con una aceleración
de 2 m/s2. ¿Cuál debe ser la
resistencia mínima del cable que lo sostiene para que suba el montacargas sin
romperse? ¿Cuál será la tensión del cable al bajar el montacargas con la
misma aceleración?
27.
Dos objetos de masas m1 = 10
kg y m2 = 15 kg, chocan (v1
= 4 i - 2 j m/s
, v2
= 5 i + 7 j m/s). Suponiendo que quedan unidos después del choque,
calcula la velocidad del cuerpo que sale despedido (módulo, ángulo respecto a
la horizontal). Representa el sistema antes y después del choque.
28.
Contesta las siguientes preguntas:
a)
Coeficiente de
rozamiento: Tipos, factores de que depende, unidades en cada sistema.
b)
Diferencia entre
sistemas de referencia inerciales y no inerciales.
c)
¿Qué relación
hay entre el impulso mecánico y el momento lineal.
29.
Tenemos una barra de 7 m sobre la que cuelgan dos pesos, uno en cada
extremo: en un extremo uno de 12 N y en el otro un peso de 5 N. ¿Qué fuerza
hay que realizar (módulo, dirección y sentido) y en qué posición debemos
aplicarla para que el sistema esté en equilibrio?
30.
Calcula la tensión de la cuerda y la aceleración del sistema.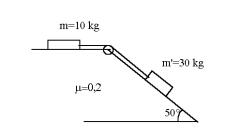
31.
Si el coeficiente de rozamiento neumáticos-suelo es de 0,6. ¿Cuál es
la velocidad máxima (km/h) con que puede tomarse una curva de 150 m de radio?
Nota: No necesitas la masa del vehículo.
32.
Calcula la velocidad (vector velocidad, módulo, dirección y sentido)
que lleva un objeto que al explotar se rompe en dos trozos de masas m1 = 12 kg y m2 = 16 kg
con velocidades respectivas de v1
= 4 i - 2 j m/s
y v2
= 5 i + 7 j m/s.
33.
Contesta las siguientes preguntas:
a)
¿Qué es la presión? Qué unidades
se utilizan.
b)
Diferencia entre sistemas de referencia inerciales y no inerciales.
c)
¿Qué relación hay entre el impulso mecánico y el momento lineal.
34.
Calcula la longitud que debe tener una barra que sostiene dos pesos para
que se cumplan las siguientes condiciones:
a)
Uno de los pesos (primer peso) es una masa de 20 kg.
b)
Para equilibrar el sistema debemos hacer una fuerza de 350 N.
c)
La distancia del segundo peso al punto de equilibrio es de 0,5 m.
35.
Calcula la tensión de la cuerda y la aceleración del sistema.
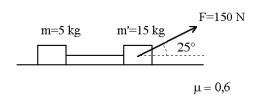
36.
Si el coeficiente de rozamiento neumáticos-suelo es de 0,7. ¿Cuál es
la velocidad máxima (km/h) con que puede tomarse una curva de 175 m de radio
sin peralte? Nota: No necesitas la masa del vehículo.
37.
Calcula la velocidad (vector velocidad, módulo, dirección y sentido)
que lleva un objeto que al explotar se rompe en dos trozos de masas m1 = 15 kg y m2 = 6 kg
con velocidades respectivas de v1
= -4 i - 2 j m/s
y v2
= 5 i + 7 j m/s.
38.
Contesta las siguientes preguntas:
a)
¿Qué es un par de fuerzas? ¿En qué unidades se expresa en el Sistema
Internacional?
b)
¿Qué diferencia hay entre masa inercial y masa gravitatoria?
c)
Tenemos un objeto situado sobre una mesa que se encuentra sobre una
superficie horizontal. Dibuja el sistema, las fuerzas que actúan y señala cuáles
son las parejas acción-reacción.
39. Observa el dibujo y calcula la aceleración del sistema.
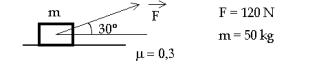
40.
Sea un peso de masa 10 kg colgado de una cuerda. Calcular la tensión del
hilo cuando el conjunto asciende o desciende con una aceleración de 6 m/s2.
41.
Una pelota cuya masa es 200 g, se mueve perpendicularmente hacia una
pared vertical con una velocidad de 25 m/s. Si la pelota choca elásticamente
con la pared y rebota sin perder velocidad, calcular el impulso que recibe la
pared durante el choque.
42.
Calcula la tensión de la cuerda y la aceleración del sistema.
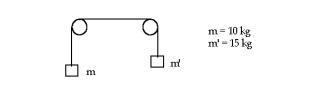
43.
Contesta las siguientes preguntas:
a)
Nombra los cuatro tipos de interacciones que se conocen.
b)
¿De qué factores depende el rozamiento?
c)
Demuestra que el coeficiente de rozamiento estático entre un objeto
situado sobre una superficie horizontal y dicha superficie, es igual a la
tangente del ángulo que debe inclinarse la citada superficie para que comience
a moverse el objeto.
44. Observa el dibujo y calcula la aceleración del sistema.
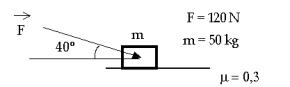
45.
Un cable de acero resiste una carga máxima de 500 kg. ¿Cuál será la
aceleración máxima con que se puede elevar un peso de 450 kg de masa, colgado
de este cable, antes de que se rompa?
46.
Un patinador de 70 kg está parado en el hielo y lanza una piedra de 3 kg
en dirección horizontal con una velocidad de 8 m/s. Calcular la velocidad de
retroceso del patinador. ¿La velocidad de retroceso sufrirá modificaciones si
existe rozamiento? Razona la respuesta.
47. Calcula la tensión de la cuerda y la aceleración del sistema.
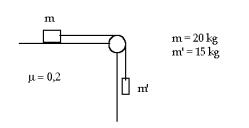
48.
Contesta las siguientes preguntas:
a)
¿Qué es un par de fuerzas? ¿En qué unidades se expresa en el Sistema
Internacional?
b)
¿Qué diferencia hay entre masa inercial y masa gravitatoria?
c)
Demuestra que el coeficiente de rozamiento estático entre un objeto
situado sobre una superficie horizontal y dicha superficie, es igual a la
tangente del ángulo que debe inclinarse la citada superficie para que comience
a moverse el objeto.
49. Observa el dibujo y calcula la aceleración del sistema.
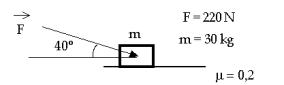
50.
Un cable de acero resiste una carga máxima de 800 kg. ¿Cuál será la
aceleración máxima con que se puede elevar un peso de 550 kg de masa, colgado
de este cable, antes de que se rompa?
51.
Un patinador de 80 kg está parado en el hielo y lanza una piedra de 2 kg
en dirección horizontal con una velocidad de 5m/s. Calcular la velocidad de
retroceso del patinador. ¿La velocidad de retroceso sufrirá modificaciones si
existe rozamiento? Razona la respuesta.
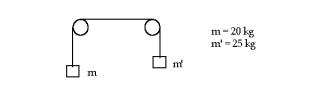
52.
Calcula la tensión de la cuerda y la aceleración del sistema.
[1] Estas preguntas se han publicado para que el alumno/a se ejercite en los bloques estudiados. Los futuros controles pueden diferir de lo aquí expuesto.
|
|