Volver

REPASO DE DINÁMICA, ROZAMIENTO

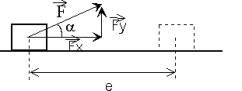
Rozamiento.

Es la fuerza que aparece en la superficie de contacto de dos cuerpos cuando se intenta deslizar uno sobre otro. La fuerza de rozamiento entre dos cuerpos se debe a que la superficie de contacto nunca es perfectamente lisa, sino que presenta unas pequeñas rugosidades imperceptibles a simple vista, rugosidades que , al encajarse unas con otras, ofrecen una resistencia al movimiento. Las principales leyes del rozamiento son:

          1.  La fuerza de rozamiento es siempre de sentido contrario a la fuerza que empuja al cuerpo.

          2.  El valor de la fuerza de rozamiento es siempre menor o, a lo sumo, igual que el de la fuerza que empuja al cuerpo.

          3.  La fuerza de rozamiento es prácticamente independiente de la superficie de contacto.

          4.  La fuerza de rozamiento depende de la naturaleza de los cuerpos en contacto, así como del estado en que se encuentren sus superficies.

          5.  La fuerza de rozamiento es directamente proporcional a la fuerza normal (perpendicular) que actúa entre las superficies en contacto. En el caso más frecuente, cuando un cuerpo se desliza por un plano horizontal, la fuerza normal es el peso del cuerpo. Sin embargo, no siempre es así; por ejemplo, cuando el cuerpo se halla sobre un plano inclinado.

          6.  Para un mismo par de cuerpos, el rozamiento es mayor en el momento del arranque que cuando se ha iniciado el movimiento.

          7.  La fuerza de rozamiento es prácticamente independiente de la velocidad con que se desplaza un cuerpo sobre el otro.

Coeficientes de rozamiento.

          Coeficiente estático de rozamiento (m_s) de un par de cuerpos es la máxima fuerza de rozamiento (FR) que puede aparecer entre ellos por cada unidad de fuerza normal (N): m_s=F_r /N

Donde F_r  sería el valor más pequeño de la fuerza que hay que realizar para poner en movimiento un cuerpo.

          Coeficiente cinético de rozamiento (m_k) de un par de cuerpos es la fuerza de rozamiento que aparece entre ellos (F_r) por cada unidad de fuerza normal (N), cuando se desplaza uno sobre otro con movimiento uniforme: m_k = F_r /N

          Ambos coeficientes de rozamiento son adimensionales; es decir, no tienen unidad.

Movimiento de un cuerpo por un plano inclinado.

          Un caso particular, de relativo interés en el estudio de movimientos de cuerpos sometidos a rozamientos, es el de un cuerpo situado en un plano inclinado, sobre el cual -independientemente de otras posibles fuerzas- actúan el propio peso del cuerpo y la fuerza de rozamiento con el plano.

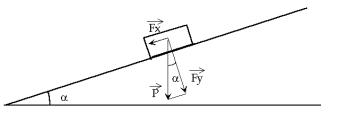
          Consideremos el cuerpo de la siguiente figura, que se apoya sobre un plano inclinado, y sea que deseamos determinar el mínimo ángulo de inclinación (a) que deberá tener el plano, para que el cuerpo se deslice por acción de su propio peso. Descomponiendo el peso en dos componentes rectangulares según el movimiento sobre el plano:

          La fuerza N origina una fuerza de reacción en el plano inclinado, que la equilibre. Además, motiva una fuerza de rozamiento, cuyo valor máximo es:

          Para que comience el movimiento, se debe verificar que la fuerza F_X  alcance justamente el valor de la fuerza de rozamiento, esto es:

          Para calcular la aceleración deberemos hallar la resultante de fuerzas del sistema y aplicar la segunda ley de Newton:    F = m·a

Ejercicios

          1.  Los coeficientes estático y cinético de rozamiento entre un cuerpo y el suelo son 0,4 y 0,3, respectivamente, siendo la masa del cuerpo 60 kg. Calcular si una fuerza de 30 kgf sería capaz de arrastrarlo y, en caso afirmativo, determinar la aceleración del movimiento resultante.

          2.  Se coloca un cuerpo en un plano de 30º de inclinación, siendo 0,4 y 0,3 los coeficientes de rozamiento estático y cinético, respectivamente. Averiguar si el cuerpo se deslizará por el plano y, en caso afirmativo, calcular con qué aceleración lo hará.

          3.  Para que una caja de madera de 120 kgf, apoyada en el suelo, comience a moverse, se requiere una fuerza horizontal de 50 kgf. Calcular el coeficiente estático de rozamiento entre la caja y el suelo.

          4.  Calcular el peso de una caja, sabiendo que para arrastrarla por el suelo, se requiere una fuerza mínima de 80 kgf, siendo 0,8 el coeficiente cinético de rozamiento. Calcular la aceleración que adquiere si se le aplica una fuerza de 100 kgf.

          5.  El coeficiente cinético de rozamiento entre el suelo y el bloque de la figura es de 0,4. Calcular la aceleración en cada uno de los casos indicados, sabiendo que el bloque pesa 100 kgf.

          6.  Sobre un plano de 30º de inclinación, se coloca un cuerpo. Calcular la aceleración con que desciende, sabiendo que el coeficiente cinético de rozamiento entre las dos superficies en contacto es 0,2.

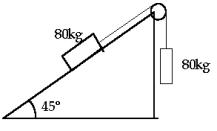
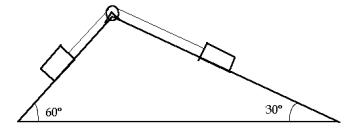
          8.  Calcular la aceleración y la tensión del sistema de la figura 6, sabiendo que el coeficiente de rozamiento cinético entre ambos cuerpos y el suelo es de 0,2 y que ambos cuerpos tienen una masa de 80 kg.

   Volver