Solución al control realizado el 28-11-02
·
La velocidad instantánea de un móvil, medida en unidades del S.I., que describe una trayectoria plana es:
![]()
a) Calcula el valor numérico de la
velocidad en los instantes t = 2 s y en t = 3 s.
b) Halla el vector aceleración media
en ese intervalo de tiempo.
Solución
a) Para t = 2 s:
![]()
![]()
Para t = 3 s:
![]()
![]()
b) Vector aceleración media en el intervalo de tiempo Dt = 3 – 2 = 1 s:
![]()
·
El gráfico siguiente representa un móvil situado
en el origen de coordenadas, que tiene las velocidades constantes que se
indican según los ejes cartesianos:
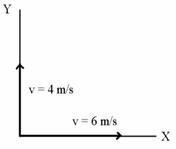
Calcula:
a) El
vector de posición del móvil para t = 3 s.
b) El
módulo del vector velocidad.
Solución
a) Las componentes cartesianas del vector velocidad son:
![]()
El vector de posición para t = 3 s es:
![]()
El móvil se encuentra en la posición (12,18) en el instante t = 3 s.
b) el módulo de la velocidad es:
·
Se lanza un proyectil con una velocidad
inicial de 120 m/s bajo un ángulo de 30º con la horizontal. Calcula:
a) La altura máxima que alcanza.
b) Su alcance máximo.
c) La velocidad (vector, módulo, dirección) a los ocho segundos del
lanzamiento.
Solución
a) La altura máxima que alcanza el proyectil
sobre el nivel del punto de lanzamiento es:
![]()
b) El alcance máximo es:
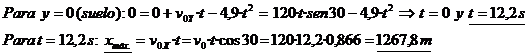
c) La ecuación de la altura del proyectil sobre el suelo es:
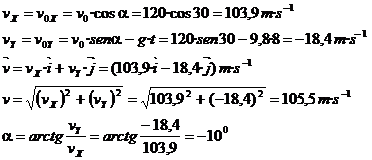
·
Un automovilista alcanza la velocidad de 90
km /h en 15 s, acelerando uniformemente desde el reposo en una pista circular
de 120 m de diámetro. Calcula:
a) La aceleración tangencial.
b) El espacio recorrido en los
primeros 15 s.
c) La aceleración normal en el
instante t = 15 s.
d) La velocidad angular cuando ha
alcanzado los 90 km/h
Solución
a) v = 90 km /h = 25 m /s
Se trata de un movimiento uniformemente acelerado:
![]()
Esta aceleración, que mide el cambio de módulo de la velocidad, es la
aceleración tangencial:
![]()
b) Espacio recorrido:
![]()
c) La aceleración normal o centrípeta para t
= 15 s es:
![]()
d) La velocidad angular es:
![]()